Conic Sections
A conic section or a conic is the locus of a point which
moves in a plane in such a way that its distance from a fixed point bears a
constant ratio to its distance from a fixed straight line. The fixed point is
called focus, the fixed line a directrix, and the constant ratio is called the
eccentricity. The eccentricity is usually denoted
by e.
Axis of a conic section
The line passing through the focus and perpendicular to the
directrix is called the axis of the conic section.
Vertex of a conic section
The points where the axis meets the conic section are
called the vertices of conic section. In another words, the point of
intersection of a conic (curve) and the axis is called the vertex of the conic
section.
We have the following three
situations:
i) If e = 1, then conic section is
called a parabola.
ii) If
0 < e < 1, then conic section is called an ellipse.
iii) If
e > 1, then conic section is called a hyperbola.
Parabola
The conic section for which the value of eccentricity, i.e. e is unity, it is called a
parabola. In another words, a parabola is the locus of a point which moves in a
plane in such a way that its distance from the fixed point (the focus) is equal
to its distance from the fixed line (the directrix).
Standard form of equation of parabola
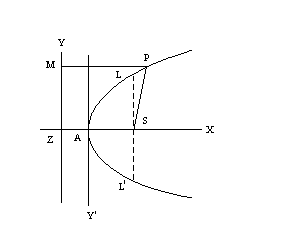
To derive the equation of parabola in standard forms
To determine the equation of a parabola in the simplest
form (the standard form), take the vertex A at the origin, the focus S on the
x–axis, so that, the axis of the parabola is the x–axis and the directrix is
parallel to the y–axis.
Let, AS = a. Thus, the co–ordinates of Z, A and S are (– a,
0), (0, 0) and (a, 0) respectively and the equation of the directrix is x + a =
0.
Let, P(x, y) be any point on the parabola. Join PS and draw
PM perpendicular to ZM. Then,
PS
= PM
i.e., PS2 = PM2
or, (x
– a)2 + y2 = (x + a)2
or, x2
- 2ax + a2
+ y2 = x2 + 2ax + a2
or, y2
= 4ax
This is true for coordinates of any point on the parabola;
hence, it is the equation of the parabola.


0 Comments