Computing Roots

Computing roots of non-linear equations 

Linear equations and some of the some of the quadratic equations can be solved easily. These equations has roots in integers or terminating decimals. But some non-linear equations cannot solved easily and their roots are repeating decimals or  non-terminating decimals. The roots of such equations can be approximate only. There are various methods to approximate the roots of such equations. 

Here, we discuss the following two methods:

1. Bisection method 

2. Newton's Raphson's method 

Bisection Method of Finding Roots

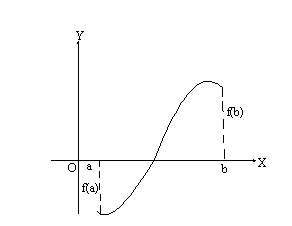
The bisection method is a root finding algorithm for the function f(x) = 0 which is based on following theorem. “If f(x) is continuous for x between a and b and if f(a) and f(b) have opposite signs, then there exists at least one real root of f(x) between a and b”.

Procedure of finding roots

Suppose that a continuous function f(x) is negative at x = a and positive at x = b. So, there is at least one root between a and b. Let us divide the interval

 

[a_, b] into two sub-intervals [a, x₁] and [x₁, b], where x₁= (a+b)/2 is taken as first approximation. If we calculate f(x₁), then there are three possibilities:

i) f(x₁) = 0                    

ii) f(x₁) > 0   

iii) f (x₁) < 0

Case (i) If f(x₁) = 0, then x₁ is required root and process is terminated.

Case (ii) If f(x₁)< 0, then the root lies between x₁ and b. In this case we again bisect the interval [x₁, b] and obtain its point of bisection x₂ as second approximation. Continuing the process of bisection and we obtain successive approximation of the root to desired accuracy.

Case (iii) If f(x₁) > 0 then the root lies between a and x₁. In this case we bisect the interval [x₁, b] and obtain the successive approximation of roots.

 

Worked out Examples

1.     Show that the equation f(x) = x³ - x - 4 has two negative roots and one positive root, and find the positive root correct to three places of decimal.

Solⁿ:    Here, f(x) = x³ - x - 4 has one change in sign Þ one positive root and

f(-x) = - x³ + x - 4 has two change in sign Þ two negative roots.

            Again, f(1) = 1³ - 1 - 4 = - 2 and f(2) = 2³ - 2 - 4 = 2

So, f(1) and f(2) has opposite sign Þ one root between 1 and 2.

So, we use the bisection method in the interval 1 < x < 2.

a	b	x =	f (x)
1.00000 1.50000 1.75000 1.75000 1.75000 1.78125 1.78125 1.79687 1.79296 1.79491 1.79589 1.79638	2.00000 2.00000 2.00000 1.87500 1.81250 1.81250 1.79687 1.78906 1.79687 1.79687 1.79687 1.79687	1.50000 1.75000 1.87500 1.81250 1.78125 1.79687 1.78906 1.79296 1.79491 1.79589 1.79638 1.796662	- 2.12500 - 0.3902 0.71679 1.14184            - 0.12960 0.00477 - 0.06276 - 0.2913 - 0.02513 - 0.00375 - 0.00050 - 0.00167

 

                Approximate value of the root to three places of decimal is 1.796.

Newton’s Raphson method

Let x₀ denote the known approximate value of the root of f(x) = 0 and let h be the difference between the true root a and the approximation value.

Then a = x₀ + h