General
equation of second degree
The
equation of the form ax2 + 2hxy + by2 + 2gx + 2fy + c = 0
is the general equation second degree in x and y.
The
pair of straight lines A1x + B1y + C1 = 0 and
A2x + B2y + C2 = 0 can always be put in the
form of second degree equation but the converse is not always true.
Homogeneous equation of second degree
The
equation of the form ax2 + 2hxy + by2 = 0 is the called
homogeneous equation of second degree in x and y. The homogeneous equation of
second degree always represents a pair of straight lines passing through the
origin.
Introduction
Consider two equation of straight lines
a1x
+ b1y + c1 = 0 ….(i)
and a2x + b2y + c2 = 0 …(ii)
The combined equation of the above equation is
(a1x
+ b1y + c1) (a2x + b2y + c2)
= 0 ….(iii)
The
coordinates of any point lying on lines (i) and (ii) will satisfy the equation
(iii). Conversely, the coordinates of any point lying on equation (iii) also
satisfy (i) or (ii) or both.
Now, on
simplification of equation (iii) yields, a1a2x2
+ (a1b2 + a2b1) xy + b1b2
y2 + (a1a2 + a2c1)x + (b1c2
+ b2c1)y + c1c2 = 0, which can also
be written as
ax2 + 2hxy + by2 + 2gx + 2fy + c = 0
where, a = a1a2, 2h = a1b2
+ a2b1, b = b1b2, 2g = a1c2+
a2c1,
2f = b1c2
+ b2c1 and c = c1c2.
Hence
every equation of pair of line is a second degree equation.
Note: The equation ax2 + 2hxy + by2
+ 2gx +2fy + c = 0 is called general equation second degree in x and y.
Theorem
The homogeneous equation of second degree
in x and y represents a pair straight
line passing through the origin.
The homogeneous equation of second
degree in x and y is
ax2
+ 2hxy + by2 = 0.
The equation can be written as
Angle between Lines
Represented by ax2+2hxy+by2 = 0
Let, y
= m1x .....(i)
and, y = m2x .....(ii)
be
equations of two lines represented by the equation ax2 + 2hxy+ by2
= 0.
Bisectors of the angles between the lines represented by
ax2 +
2hxy + by2 = 0
Condition that the General Equation of Second Degree to Represent a Pair of Lines
The general equation of second degree in x and y is;
ax2
+ 2hxy + by2 + 2gx + 2fy + c = 0 (a ¹ 0)
The equation may be written as a quadratic in x, as
ax2
+ 2x(hy + g) + by2 + 2fy + c = 0
Solving for x;
These equations will be linear only if (hy + g)2 – a(by2
+ 2fy + c) be perfect square,
i.e., (h2 – ab) y2 + 2(gh
– af)y + (g2 – ac) be a perfect square
i.e., {2(gh – af)2} – 4(h2
– ab) (g2 – ac) = 0
i.e., (gh – af)2 – (h2 –
ab) (g2 – ac) = 0
i.e., g2h2 – 2afgh + a2f2
–g2h2+ h2ac + g2ab - a2bc = 0
i.e., a(abc + 2fgh – af2 – bg2
– ch2) = 0
Since a ¹ 0, the required conditions is abc + 2fgh – af2
– bg2 – ch2 = 0.
If a = 0 but b ¹ 0, then
the given equation can be expressed as a quadratic in y and we can find the
condition in the same way.
Equation of the Pair of Lines Joining Origin to the Points
of Intersection of Line and Curve
Let lx + my = n ….(i)
be a straight line and
ax2 + 2hxy + by2
+ 2gx + 2fy + c = 0 …(ii)
be the curve.
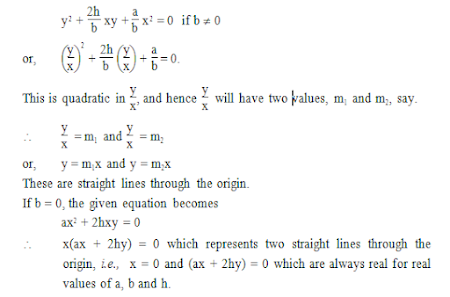









0 Comments