Course Outlines
·
Review the three dimensional Cartesian
co-ordinates
·
Cylindrical and spherical co-ordinates of a
point
·
General equation of first degree
·
Linear equation of a plane
·
Angle between two planes
·
Angle between a line and a plane
·
Plane through three points
·
Plane through the intersection of two planes
·
Length of perpendicular from a point to a
plane
·
Bisectors of angles between two planes
·
Pair of planes
·
Conditions for homogeneous second degree
equation to represent a pair of planes
·
Angle between two planes represented by a
second degree homogeneous equation.
Coordinates in Space
In a plane the position of a point is determined by an ordered pair (x, y) of real numbers obtained with reference to two straight lines in the plane generally at right angles. The position of a point in space is, however, determined by an ordered triad (x, y, z) of real numbers.
Distance between Two Points
Direction Cosines of a Line
Let a, b, g be the angles which any line makes with the positive directions of the co-ordinates axes. Then cos a, cos b, cos g are called the direction cosines of the given line and are generally denoted by l, m, n respectively.
A useful relation If O be the origin of and (x, y, z) be the co-ordinates of a point P, then x = lr, y = mr, z = mr, l, m, n being the direction cosines of the line OP and r, the length of the segment OP.
Through the point P draw the line PL perpendicular to the X-axis so that OL = x.
From the right-angled triangle OPL, we have
Þ x/r = l Þ x = lr.
Similarly, we have
y = mr, z = nr
Relation Between Direction Cosines
If l, m, n are the direction cosines of a line,
l2 + m2 + n2 = 1,
i.e., the sum of the squares of the direction cosines of every line is unity. Let OP be drawn through the origin parallel to the given line so that l, m, n are the cosines of the angles which the line OP makes with the co-ordinate axes OX, OY, OZ respectively.
Let (x, y, z) be the co-ordinates of any point P on this line.
Let OP = r.
We have x = lr, y = mr, z = nr.
Squaring and adding, we obtain
x2 + y2 + z2 = (l2 + m2 + n2)r2
Þ r2 = OP2 = x2 + y2 + z2 = (l2 + m2 + n2)r2
Þ l2 + m2 + n2 = 1.
(i) The given lines are perpendicular
Þ q = 900
Þ cos q = 0
Þ a1a2 + b1b2 + c1c2 = 0.
(ii) The given lines are parallel
Þ the lines through the origin drawn parallel to the lines coincide,
Þ the direction cosines of the lines are the same.
Þ the direction ratios of the lines are proportional.
Worked Out Examples
Plane
A locus is said to be a plane if it is such
that if P and Q are any two points on the locus, then every point on the line
segment PQ is also a point on the locus.
General Equation of first Degree
An equation of the first degree x, y, z is of
the form
ax + by + cz + d = 0,
where a, b, c and d are constants and a, b, c
are not all zero. The condition that a, b, c are not all zero is equivalent to
a2 + b2 + c2 ¹ 0.
Theorem:
Every equation of the first degree in x, y and z represents a plane.
Proof:
The general equation of first degree in x, y,
z is
ax + by + cz + d = 0,
where a, b, c and d are constants and a, b, c
are not all zero.
The locus of this equation will be a plane if
every point of this line joining any two points on the locus also lies on the
locus.
Let P(x1, y1, z1)
and Q(x2, y2, z2) be two points on the locus,
so that
ax1
+ by1 + cz1 + d = 0 …..(i)
and ax2 + by2 + cz2
+ d = 0 …..(ii)
Multiplying (ii) by k and adding to (i), we
get



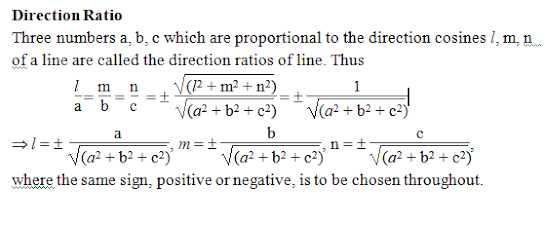








































































0 Comments